| “슈퍼 하이젠베르그 한계” 및 “하이젠베르그 한계”의 양자 정밀 측정 동시 달성 | ||
|
||
 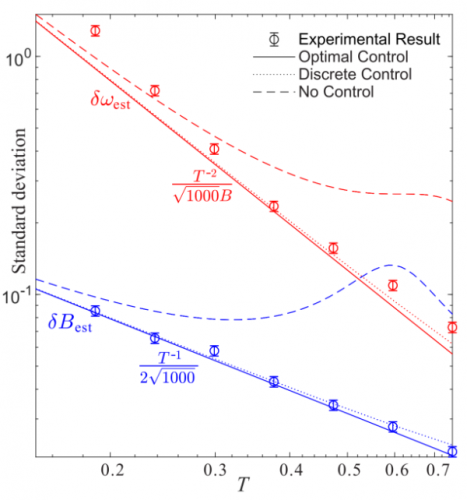 중국과학기술대학교 Guo Guangcan(郭光燦) 원사 연구팀의 Li Chuangfeng(李傳鋒), Xiang Guoyong(項國勇) 연구팀은 홍콩중문대학교 Yuan Haidong(袁海東) 교수연구팀과 공동으로 양자 정밀 측정 실험에서 최초로 두개 매개변수가 동시에 각각 “슈퍼 하이젠베르그 한계(Super Heisenberg limit)”와 “하이젠베르그 한계”의 최적 측정을 달성했다. 해당 연구 성과는 국제학술 "Physics Review Letters"의 온라인 표지 기사로 게재되었다. 정밀 측정의 정확도는 소모되는 자원의 증가에 따라 향상된다. 수학적으로 Tk로 설명되며 그중, T는 자원(예를 들어 측정 시간)이고, k는 다양한 측정 방법의 장단점을 평가하는 가장 중요한 표준 정확도 증가 순서이다. 위상 추정, 자력계 및 양자 자이로스코프 등 많은 응용에서 전형적 측정 방법과 양자 측정 방법의 k는 각각 0.5와 1이며 각각 “산탄 잡음 한계” 및 “하이젠베르그 한계”로 불린다. 그러나, 다체 상호작용 또는 시간종속 진화가 존재할 경우, k가 1을 초과할 수 있음이 발견됐며 이를 "슈퍼 하이젠베르크 한계"라고 한다. 세가지 정확도 한계는 단일 매개변수 양자 측정 실험에서 각각 달성되었지만 그러나 하이젠베르그 불확실성 관계는 양자 역학의 근본적인 한계이며 "슈퍼 하이젠베르그 한계"의 하이젠베르그 초월 여부는 여전히 논란의 여지가 있다. 연구팀은 자체 개발한 다중 매개변수 양자 정밀측정 플랫폼을 이용하여 회전장의 강도와 주파수 두가지 매개변수를 측정하는 과정에서 “슈퍼 하이젠베르그 한계”와 “하이젠베르그 한계”의 동시 달성 여부를 연구했다.연구팀은 증강 제어의 순차 측정 기술을 심층 개발하여 다중 매개변수 시간종속 진화 측정에서 양자 시스템 동역학적 진화의 각 부분을 최적화함으로써 두개 매개변수가 동시에 각각 “하이젠베르그 한계”와 “슈퍼 하이젠베르그 한계”에 도달하는 최적 측정을 달성했다. 또한, 두가지 정확도 한계가 모두 하이젠베르그 불확실성 관계를 준수하며 모두 최적의 양자 정확도 한계임을 규명하였다. 해당 연구 성과는 양자 정밀 측정과 하이젠베르그 불확실성 관계 두 분야의 연결을 강화하고, 두개 분야의 교차 개발을 촉진하였으며 실제 측정 문제에서 잠재적 응용 가치가 있다. 정보출처 : http://www.stdaily.com/index/kejixinwen/2021-02/22/content_1082309.shtml |
- 정책동향
- 이슈리포트
- 통계DB
- 통계DB
